অজানা রাশির সূচক, গুণ ও তাদের প্রয়োগ – Class 7 Math BD 2023 – ২য় অধ্যায় (৩৩ – ৪১ পৃষ্ঠা)

আজকের
অধ্যায়ে আমরা অজানা রাশির সূচক, গুণ ও তাদের প্রয়োগ সংবলিত সমস্যা বা কাজ এর সমাধান
করব। এই অধ্যায়ে বিভিন্ন বিষয় নিয়ে আলোচনা করা হয়েছে এবং সেই সম্পর্কিত বিভিন্ন কাজ
এর সমাধান এখানে সন্নিবেশিত করেছি।

সূচক

সূচক বা exponent বোঝার জন্য পাঠ্যবইয়ে প্রথমে যে বিষয়টি আলোচনা করা হয়েছে তার হলোঃ বর্গ চিনি। চলো
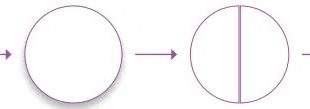
আমরা একটি বর্গাকার কাগজ নিই। [বর্গ একটি আয়ত, যার বাহুগুলো পরস্পর সমান]। চিত্রের মত
করে কাগজটিকে পরপর দুইবার (একবার দৈর্ঘ্য বরাবর ও একবার প্রস্থ
বরাবর) সমান অংশে ভাঁজ করি। এবার কাগজটি খোলার পর যে কয়টা
ছোট ঘর হলো প্রতি
ঘরে একটি করে মার্বেল রাখি। মোট কয়টি মার্বেল প্রয়োজন হলো?

শিখনঃ
একইভাবে আরেকটি
বর্গাকার কাগজকে দৈর্ঘ্য ও প্রস্থ বরাবর
সমান তিনটি অংশে পরপর ভাঁজ করি। তোমাদের সুবিধার জন্য ভাঁজ বরাবর কাগজে স্কেলের দাগ দিয়ে ঘর করে নিতে
পারো। এবার প্রতি ছোট ঘরে একটি মার্বেল বসালে কয়টি মার্বেল লাগবে?

সমাধানঃ

বর্গাকার
কাগজটিকে দৈর্ঘ্য ও
প্রস্থ বরাবর সমান তিনটি অংশে পরপর ভাঁজ করলে কাজটিতে প্রতি সারিতে ৩টি
করে ছোট বর্গ বা ঘর পাওয়া যায় এবং মোট সারির সংখ্যা হয় ৩টি।

তাহলে,
মোট ছোট ঘরের সংখ্যা = ৩×৩ টি = ৩^২ টি = ৯ =টি।

অর্থাৎ,
ছোট ঘরে একটি করে মার্বেল বসালে মার্বেল লাগবে ৯টি।

শিখনঃ
একই ভাবে দৈর্ঘ্য ও প্রস্থ বরাবর
সমান চারটি, পাঁচটি, ছয়টি ও সাতটি করে
ভাঁজের জন্য কয়টি মার্বেল লাগে তা দিয়ে নিচের
ছকটি পূরণ করো। (পাঠ্যবইয়ের ছকঃ ১.১)

সমাধানঃ

সূত্রঃ
বর্গাকার কাগজকে দৈর্ঘ্য ও প্রস্থ বরাবর সমান যত অংশে ভাঁজ করা হবে ঠিক ততো অংশে বর্গের
সমান ছোট বর্গ বা ঘর পাওয়া যাবে।

দৈর্ঘ্য ও প্রস্থ বরাবর সমান অংশ সংখ্যা	মার্বেল সংখ্যা	দৈর্ঘ্য ও প্রস্থ বরাবর সমান অংশ সংখ্যা	মার্বেল সংখ্যা
2	4	5	25
3	9	6	36
4	16	7	49

একক
কাজঃ এখন কাগজটিকে
দৈর্ঘ্য ও প্রস্থ বরাবর
৮ ভাঁজ করে দাগ টেনে দেখো ঘর সংখ্যা কত
হয়?

সমাধানঃ
ভাঁজ করে স্কেল দিয়ে দাগ টেনে নিজে চেষ্টা করো।

শিখনঃ
একটি বর্গাকার
কাগজকে দৈর্ঘ্য ও প্রস্থ বরাবর
সমান অংশে ভাঁজ করে মার্বেল বসানোর খেলার মাধ্যমে কোনটি পূর্ণবর্গ সংখ্যা এবং কোনটি পূর্ণবর্গ সংখ্যা নয় যাচাই করো।

সমাধানঃ

তোমরা
কাগজ ভাঁজের খেলার মাধ্যমে কোনটি পূর্ণবর্গ বা পূর্ণবর্গ নয় তা যাচাই করবে। আমরা নিচের
ছকে প্রদত্ত যাচাই করণের ফলাফল পূর্ণবর্গ হলে √ এবং পূর্ণবর্গ না হলে X চিহ্ন দ্বারা প্রকাশ
করে দেখালাম।

সংখ্যা	2	5	7	82	36	45	81	56	12
সংখ্যাটি কি পূর্ণবর্গ?	X.	X.	X.	X.	√	X.	√	X.	X.

দলগত
কাজঃ আমরা বর্গসংখ্যা
কোনগুলো চিনলাম। এবার তোমাদের ক্লাস রোলের শেষ অঙ্ক অনুযায়ী দাঁড়িয়ে ১০ টি সারি
করো। এখন তোমরা নিজেদের মধ্যে সারির পরিবর্তন করে বর্গসংখ্যার সমান করে একেকটি সারি বানাও।

রোলের শেষ অঙ্ক	0	1	2	3	4	5	6	7	8	9
		🕴	🕴 🕴	🕴 🕴 🕴	🕴 🕴 🕴 🕴	🕴 🕴 🕴 🕴 🕴	🕴 🕴 🕴 🕴 🕴 🕴	🕴 🕴 🕴 🕴 🕴 🕴 🕴	🕴 🕴 🕴 🕴 🕴 🕴 🕴 🕴	🕴 🕴 🕴 🕴 🕴 🕴 🕴 🕴 🕴

সমাধানঃ

এখানে,
এখানে শেষ সারিতে ৯ জন শিক্ষার্থী আছে।

৯
= ৩×৩ = ৩^২ অর্থাৎ ৯ একটি পূর্ণবর্গ সংখ্যা।

তাহলে,
৮ জনের সারিতে ১ জনের সারীর শিক্ষার্থী যোগ দিলে মোট ৯ জন হবে এবং ৯ পূর্ণবর্গ বলে
নতুন সারিটি প্রদত্ত শর্ত পূরন করবে।

এভাবে,

৭
জনের সারিতে ২ জনের সারির শিক্ষার্থী, ৬ জনের সারিতে ৩ জনের সারির সকলে, ৫ জনের সারিতে
৪ জনের সারির সকলে যোগ দিয়ে ৯ জন করে নতুন সারি গঠন করবে।

শিখন
ফলাফলঃ

আয়তক্ষেত্রের
ক্ষেত্রফল = দৈর্ঘ্য×প্রস্থ

বর্গও
একটি আয়তক্ষেত্র যা দৈর্ঘ্য ও প্রস্থ সমান।

অতএব
বর্গের ক্ষেত্রফল = দৈর্ঘ্য×দৈর্ঘ্য = (দৈর্ঘ্য)^২ = x²

ঘনকঃ

একক
কাজঃ তিনটি ও চারটি করে ছোট ঘনক নিয়ে বড় ঘনক বানাও
এবং কয়টি ছোট ঘনক লাগে দেখো।

সমাধানঃ

৩টি
করে ছোট ঘনক নিয়ে বড় ঘনক বানাতে ছোট ঘনক লাগবে = ৩×৩×৩ = ৩^৩ = ২৭ টি।

৪টি
করে ছোট ঘনক নিয়ে বড় ঘনক বানাতে ছোট ঘনক লাগবে = ৪×৪×৪ = ৪^৩ = ৬৪ টি।

শিখনঃ
ছবির প্রতিটি রুবিক্স কিউব তৈরি করতে মোট কতগুলো ছোট ঘনক প্রয়োজন হয়েছে তা নির্ণয় করে
ছক ৫.১ পূরণ
করো।

সমাধানঃ

ছক
৫.১

রুবিক্স কিউব	দৈর্ঘ্য, প্রস্থ ও উচ্চতা বরাবর ছোট ঘনক সংখ্যা	মোট কতগুলো ছোট ঘনক প্রয়োজন
a	2	2×2×2 = 23 = 8
b	3	3×3×3 = 33 = 27
c	4	4×4×4 = 43 = 64
d	5	5×5×5 = 53 = 125
e	9	9×9×9 = 93 = 729
f		8×8×8 = 83 = 512
g		7×7×7 = 73 = 343
h		6×6×6 = 63 = 216

একক
কাজঃ নিচের টেবিলটি পূরণ করোঃ

বরাবর একই সংখ্যা বা রাশির গুণ	ভিত্তি	সূচক	শক্তি বা ঘাত	মান
2.2.2.2.2	2	5		32
x.x.x.x
4.4.4
	5	3

সমাধানঃ

বরাবর একই সংখ্যা বা রাশির গুণ	ভিত্তি	সূচক	শক্তি বা ঘাত	মান
2.2.2.2.2	2	5		32
x.x.x.x	x	4
4.4.4	4	3		64
5.5.5	5	3		125
6.6	6	2		36

একক
কাজঃ

সূচকের
গুণ এবং ভাগের নিয়ম অনুযায়ী নিচের রাশিগুলোকে সরল করো।

1)
3²×9²

2)
5³×25^-2

3)	s13 —-
4)	s13t-4 ——
5)	2s13t-4 ——-

সমাধানঃ

1)

3²×9²

=
3³×(3²)²

=
3²×3⁴

=
3²⁺⁴

=
3⁶

=
3×3×3×3×3×3

=
729

2)

 5³×25^-2

=
5³×(5²)^-2

=
5³×5^-4

=
5^-1

=
¹/₅

3)

 s¹³

—–

 s⁵

=
s^13-5

=
s⁸

4)

——

=
s^13-5.t^-4-14

=
s⁸.t^-18

    s⁸

=
—-

    t¹⁸

5)

———

=
———-

    2²s⁵t^-14

=
2^1-2.s^13-5.t^-4+14

=
2^-1.s⁸.t¹⁰

=
½.s⁸.t¹⁰

একক
কাজঃ

সূচকের
গুণ ও ভাগের নিয়ম অনুসারে সরল করোঃ

১.
(5²)³

২.
(a^-4)³

৩.
(3³a^-5b³)³

সমাধানঃ

১.

(5²)³

=
5^2×3

=
5⁶

২.

(a^-4)³

=
a^-4×3

=
a^-12

৩.

(3³a^-5b³)³

=
3^3×3a^-5×3b^3×3

=
3⁹a^-15.b⁹

    S^5×3

=
——

    S¹⁵

=
——

    3¹²

   

    st^7×3

=
——–

    s³.t²¹

=
——–

     r³.t⁹

    s³.t^21-9

=
———

      r³

    s³.t¹²

=
——-

      r³

একক
কাজঃ

x=0
হলে, x⁰ এর মান কী হবে?

সমাধানঃ

x⁰
এর কী হবে এর জন্য আমরা একটি রাশি ধরি যা নিন্মরুপঃ

 x⁴

—-

এখন
এই রাশির মান = 1 কারন x⁴ কে x⁴ দ্বারা ভাগ করলে অর্থাৎ একই
সংখ্যাকে সেই সংখ্যা দ্বারা ভাগ করলে ভাগফল 1 হয়।

তাহলে,
উক্ত রাশি = x^4-4 = x⁰ = 1

আবার,

 x⁴

—-

     0

=
—-

     0

কিন্তু
আমরা জানি, ⁰/₀ অসম্ভব বা হতে পারে না।

x=0
হলে, x⁰ এর অসম্ভব কিন্তু x⁰ = 1 হলে x ≠ 0

পৃষ্ঠা
৩৩ – ৪১ পর্যন্ত সমাধান এই অংশে দেওয়া হলো। বাকী অংশগুলোর লিঙ্ক নিন্মরুপঃ

পৃষ্ঠা ৪১ – ৫২

পৃষ্ঠা ৫৩ – ৫৭ 

পৃষ্ঠা ৫৮ – ৫৮

এই অধ্যায়ের সূচীর লিঙ্কঃ

Class 7 Math BD – 2023

৭ম শ্রেণি ১ম অধ্যায়ঃ সূচকের গল্প