[ad_1]
অজানা রাশির
ভগ্নাংশের গল্প । বীজগণিতীয় ভগ্নাংশের
যোগ ও বিয়োগঃ
তোমরা
৬ষ্ঠ শ্রেণিতে বীজগণিতীয় রাশির যোগ ও বিয়োগ সম্পর্কে
শিখেছ। আবার পাটীগণিতীয় ভগ্নাংশ সম্পর্কেও জেনেছ। এসো এবার আমরা বীজগণিতীয় ভগ্নাংশের যোগ ও বিয়োগ সম্পর্কে
শিখি। এই জন্য পাঠ্যবইয়ের কর্মপত্রগুলো
অনুশীলন করো। অজানা রাশির ভগ্নাংশের গল্প অংশে আমাদের প্রথম আলোচ্য অংশ হলো বীজগণিতীয়
ভগ্নাংশের যোগ ও বিয়োগ। চল, আমরা প্রদত্ত সমস্যাগুলোর সমাধান করি।
একক
কাজ: (পৃষ্ঠা ২২১)
(প্রশ্ন
১ ও ২ এর
জন্য, যদি বৃত্তটির ক্ষেত্রফল x বর্গ একক হয়। )
১।
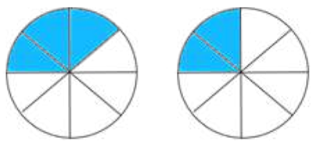
নিম্নের মডেলটি থেকে ভগ্নাংশ বের করো এবং যোগ করো।
সমাধানঃ
প্রদত্ত মডেলের
১ম বৃত্ত ক্ষেত্রের রং করা অংশের সংখ্যা 3টি এবং মোট অংশের সংখ্যা 5টি।
তাহলে, রং
করা অংশ = x এর 3/5 = 3x/5
আবার,
প্রদত্ত মডেলের
২য় বৃত্ত ক্ষেত্রের রং করা অংশের সংখ্যা 3টি এবং মোট অংশের সংখ্যা 10টি।
তাহলে, রং
করা অংশ = x এর 3/10 = 3x/10
তাহলে, প্রদত্ত
মডেল থেকে প্রাপ্ত ভগ্নাংশদ্বয় হলোঃ 3x/5 ও 3x/10
এবং ভগ্নাংশদ্বয়ের
যোগফল
= 3x/5
+ 3x/10
2×3x + 3x
=
————–
10
6x + 3x
=
————–
10
= 9x/10
২।
প্রথম বৃত্ত থেকে দ্বিতীয় বৃত্ত বিয়োগ করোঃ
সমাধানঃ
১ম বৃত্তের
রং করা অংশের সংখ্যা 3টি এবং মোট অংশের সংখ্যা 8টি।
তাহলে, রং
করা অংশ = x এর 3/8 = 3x/8
আবার,
২য় বৃত্তের
রং করা অংশের সংখ্যা 2টি এবং মোট অংশের সংখ্যা 8টি।
তাহলে, রং
করা অংশ = x এর 2/8 = 2x/8
তাহলে, দুইটি
বৃত্ত থেকে প্রাপ্ত ভগ্নাংশদ্বয় হলোঃ 3x/8 ও 2x/8
তাহলে, ভগ্নাংশদ্বয়ের
যোগফল (১ম বৃত্ত – ২য় বৃত্ত)
= 3x/8
– 2x/8
3x – 2x
=
————–
8
= x/8
৩।
x-দৈর্ঘ্যের একটি বেতের 1/3 অংশ
লাল স্কস্টেপ দ্বারা মোড়ানো, ¼ অংশ কালো স্কস্টেপ দ্বারা মোড়ানো এবং অবশিষ্ট অংশ সাদা স্কস্টেপ দ্বারা মোড়ানো হলে, সাদা স্কস্টেপ দ্বারা মোড়ানো বেতের পরিমাণ কত?
সমাধানঃ
বেতের দৈর্ঘ্য
= x
বেতটি লাল
স্কস্টেপ দ্বারা মোড়ানো x এর 1/3 অংশ = x/3
অংশ
বেতটি কালো
স্কস্টেপ দ্বারা মোড়ানো x এর 1/4 অংশ = x/4
অংশ
অতএব,
লাল ও কালো
স্কস্টেপ দ্বারা মোড়ানো অংশ
= x/3
অংশ + x/4 অংশ
4x + 3x
=
———— অংশ
12
= 7x/12
অংশ
তাহলে,
বেতটির অবশিষ্ট
সাদা স্কস্টেপ দ্বারা মোড়ানো অংশ
= x – 7x/12
অংশ
12x – 7x
=
———– অংশ
12
= 5x/12
অংশ
৪.
হেনা ৭ম শ্রেণির শিক্ষার্থী।
সে তার বাড়ির উঠানে 1/3
অংশে সবজি চাষ, ¼ অংশে ফুলের বাগান করল। উঠানের কত অংশ খালি
রইল তা বীজগণিতীয় পদ্ধতিতে
বের করো।
সমাধানঃ
মনে করি,
হেনার উঠানের সম্পূর্ণ অংশ = x
তাহলে, হেনা
সবজি চাষ করে x এর 1/3 অংশে = x/3 অংশে
এবং ফুলের
বাগান করল x এর ¼ অংশে = x/4 অংশে
অতএব, হেনা
সবজি চাষ ও বাগান করল
= (x/3
+ x/4) অংশে
4x+3x
=
———- অংশে
12
= 7x/12
অংশে
তাহলে, চাষ
বিহীন বা খালি অংশ
= x – 7x/12 অংশ
12x-75
=
———— অংশ
12
= 5x/12
অংশ
= x এর 5/12
অংশ
= উঠানের
5/12 অংশ।
অজানা রাশির
ভগ্নাংশের গল্প । বীজগণিতীয় রাশির
ভাগঃ
আজানা রাশির
ভগ্নাংশের গল্প এর এই অংশে আমরা বীজগণিতীয় ভাগ সম্পর্কিত সমস্যার সমাধান করব। এই জন্য
দুইটি রাশির ভাগের ক্ষেত্রে এদের চিহ্ন কিরুপ হবে তা জেনে নেই-
একই
চিহ্নযুক্ত দুটি রাশির ভাগফল (+) চিহ্নযুক্ত রাশি হবে।
বিপরীত
চিহ্নযুক্ত দুটি রাশির ভাগফল (-) চিহ্নযুক্ত রাশি হবে।
এছাড়া,
রাশির বেজ
একই কিন্তু সূচক ভিন্ন হলে তার ভাগ প্রক্রিয়া নিন্মরুপ হবেঃ
ax
÷
ay = ax-y
একক কাজঃ
ভাগ করো (পৃষ্ঠা ২২৪)
24a5
a. ———-
-18x3y2
b. ———-
-6x2y
c. ———-
-5a3c3
সমাধানঃ
24a5
a. ———-
-3a2
24
a5
= —–×—–
-3
a2
= -8×(a5-2)
= -8×a3
= -8a3
-18x3y2
b. ———-
-6x2y
-18
x3y2
= —–×———-
-6
x2y
= 3×(x3-2×y2-1)
= 3×x1×y1
= 3xy
= -8a3
c. ———-
-5a3c3
20
a3c4d2
= —–×———-
-5
a3c3
= -4×(a3-3×c4-3×d2)
= -4× a0×c1×d2
= – 4×1×c×d2
= – 4cd2
বহুপদী
রাশিকে একপদী রাশি দ্বারা ভাগ:
কাজ:
(পৃষ্ঠা ২২৭)
১ম
রাশিকে ২য় রাশি দ্বারা
ভাগ করো:
ক)
3a3b2 -2a2b3 , a2b2
খ)
20x3y + 10xy2 – 15x2y, 5xy
সমাধানঃ
ক)
(3a3b2 -2a2b3) ÷ a2b2
3a3b2 2a2b3
= ——– – ——–
a2b2 a2b2
= 3×a3-2×b2-2
– 2a2-2×b3-2
= 3×a1×b0
– 2×a0×b1
= 3×a×1
– 2×1×b
= 3a –
2b
খ)
(20x3y + 10xy2 – 15x2y) ÷ 5xy
20x3y 10xy2 15x2y
= ——- + ——– – ———
5xy 5xy 5xy
= (20/5)×x3-1×y1-1
+ (10/5)×x1-1×y2-1 – (15/5)×x2-1×y1-1
= 4×x2×y0
+ 2×x0×y1 – 3×x1×y0
= 4×x2×1
+ 2×1×y – 3×x×1
= 4x2
+ 2y – 3x
এই অধ্যায়ের অংশসমূহঃ
পৃষ্ঠা ২১৭-২২৪ [অজানা রাশির ভগ্নাংশের গল্প] – এই অংশে আলোচিত
পৃষ্ঠা ২২৭ – ২২৮ [গুটির খেলা পদ্ধতির ভাগ]
সপ্তম শ্রেণির অন্যন্য অধ্যায় লিংকঃ